While we may intuitively understand the crucial role of memory, knowledge and understanding in learning, it is useful to unpack in more detail the building blocks of the learning process and consider how we can use this information to support the learning and development of higher-order thinking skills such as creativity and critical thinking.
Learning in the brain
The brain is composed of nerve cells, and their basic function is to communicate with each other by transmitting and receiving signals. Our knowledge base is represented in networks of neurons, and the ability to recall any given concept (a word, an object, a procedure) is based on a synchronous activity of a specific neuronal network in response to a certain cue. The most important feature of neuronal networks is plasticity – the ability to constantly change and create new connections and patterns. This feature enables us to learn and remember. When we experience something new, our neurons respond in a certain pattern, after which they undergo consolidation to stabilise the newly activated pattern and newly created connections. This process potentially enables us to recall this piece of new information in the future.
There are a number of factors that influence the quality of learning and have implications for classroom practice:
- A new concept is always learned in association with existing knowledge
- The quantity of existing knowledge and the level to which it is interconnected influence the quality of learning (more interconnected knowledge leads to easier and faster learning)
- Connections between new and old are formed following a mutual activation – the new concept and the relevant existing knowledge are active and connected during learning
- The connections between the new concept and the prior knowledge need to be meaningful to the learner
What is meaning?
Research shows that information is much better recalled if it is processed meaningfully during learning. A new concept is considered to have meaning once it enables the brain to respond or, in other words, once the new concept is integrated with existing knowledge in a way that supports an action or a decision. For example, when a child learns the word ‘shoe’, it only becomes useful once an effective association is made with the already familiar object. Once this connection has been made, the child can understand the sentence ‘put on your shoe’ and respond to it: the new concept can now be used to execute an action.
At the basic level, learning involves attaching a concrete meaning to a meaningless concept like a word, such as the name of a person (‘Eli’), an action (‘play’) or an object (‘ball’). In order to be able to attach meaning to a new concept, we need to be able to use it – for example, to ask Eli to play ball. The recurrent successful use of a word reinforces the associations within the network, and the concept becomes more robust. Creating meaning at this basic level of learning relies on concrete experiences.
At higher levels of learning, concepts with concrete meaning are used as examples for more abstract or more general concepts. For example, if we wish to teach what ‘equal’ means, we can say ‘If Eli has one ball and Sam has one ball, then they have an equal number of balls’. We establish the meaning of the new concept ‘equal’ on the basis of already known concepts (‘ball’, ‘Eli’, ‘has’, and so on). Later, we can connect ‘equal’ with more abstract concepts such as ‘equality’ or ‘equity’.
The relationship between memorising and understanding
When we memorise, we are able to recite a certain fact like ‘4 x 3 = 12’. A student who is able to do this has a basic understanding of ‘four times three’ that allows them to use that information at a low level and in a very specific context (such as answering a question in a maths quiz), but would not demonstrate deep understanding of the concept of multiplication. To create a higher level of understanding, we need to use concrete examples (‘Eli has three baskets, and there are four balls in each basket’) and connect them explicitly (‘so we can say Eli has three times four balls’). If we repeat this example and add others, making sure that the student is practising them repeatedly and effectively, we establish an understanding of the concept of multiplication as opposed to a rote memorisation of the fact ‘4 x 3 = 12’. As a higher-level concept, it will now be useful in various situations, and can serve as a basis for future learning. Every time multiplication is used is an opportunity to practise and to receive positive feedback that helps to anchor the concept in the brain. Eventually, the student will master the concept and be able to use it effortlessly.
Memorising and understanding are not opposites but rather two components of the same thing. We can map the common terms ‘memorising’ and ‘understanding’ on to lower and higher levels of understanding respectively. Achieving understanding at each level is based on available background knowledge and the meaningful connections that are learned and practised.
Knowledge versus understanding
Knowledge is the collection of concepts represented in the brain, and understanding is the connections that they form, such that they are interrelated and dependent on each other. This highlights two important features of the way our brains learn:
- It is hierarchical: new knowledge must be built on existing knowledge
- It is based on meaning: the glue that puts the pieces together is our ability to use the new in the context of the existing
The learning process can be thought of as a pyramid, where the knowledge pieces are the bricks and the structure they form depends on understanding. The final product is dependent on both:
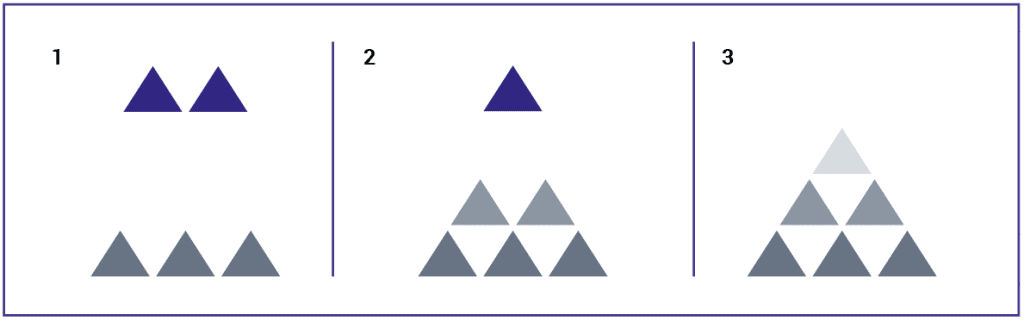
As we learn more, we create more pyramids and more opportunities for higher-order learning (where a whole pyramid becomes just a brick in a new one) and interdisciplinary learning (that is supported by several other pyramids), as illustrated in the upper section of the diagram below. When foundational knowledge and understanding are not in place, as in the lower section of the diagram, learning will not be successful because the new information cannot connect with existing knowledge.

Understanding the nature of this hierarchical and interconnected structure directs our attention to two important issues:
- The ability to engage in higher-order learning is dependent on the solid structure of well-established knowledge. This means that teaching wide and deep knowledge in meaningful ways is a crucial goal of education, especially in the age of technology and readily available information. Knowledge must be carefully learned and encoded in an individual’s brain in order to support higher-order skills: learning knowledge and structuring it are essential for meaningful understanding.
- Higher-order thinking skills, like critical thinking and creativity, are attained only on the basis of a solid body of knowledge in a specific domain. There is no benefit in teaching critical thinking or creativity as a general ‘skill’, as explained here in detail. Rather, we should build the relevant body of knowledge and then deliberately practise the way of thinking we want to students to develop.
Applications in the classroom
When students appear to be struggling to grasp new concepts, it may be because they lack either sufficient relevant background knowledge or the ability to connect it meaningfully to new material. Students who do not appear to demonstrate an understanding of concepts like multiplication or photosynthesis may actually have understood them at a low level, which is sufficient to perform only a narrow range of tasks, rather than having understood nothing at all. In order for a concept to be retained in long-term memory, it is necessary to consolidate its meaning through ongoing practice and reinforcement.
It is crucial for our students to attain higher-level understanding so that the knowledge they learn at school will be accessible and useful to them in the future. To promote deep, higher-level understanding in the classroom, it is important to focus on three basic components: new knowledge, prior knowledge and meaningful connection:
1. New knowledge: the new concept needs to be explicit, distinct, and clear
Present the new concept before beginning the learning task to establish familiarity, if possible even more than once. For example, you might write it on the board as a preview for the lesson, or mention a concept in the context of future learning. It is also important to present the new concept explicitly, clearly and distinctly to ensure processing. You can do this by:
- Explaining the concept explicitly and repeating it after a reasonable interval
- Giving a straightforward explanation, rather than letting students explore and discover (these inquiry-based activities are more appropriate at later stages)
- Presenting only one new concept at a time, so as not to overload working memory resources
2. Prior knowledge: relevant prior knowledge needs to be available and active
Prior knowledge is the base of any learning pyramid, and is essential for future learning and higher-order skills. It is important to teach a rigorous content-rich curriculum as facts are essential bricks for future pyramids. There is ample evidence to support this. If prior knowledge is not available, there is no other way but to teach it: time is better spent on teaching the basics than trying to teach new content without it.
Relevant information also needs to be active at the time of learning. It is tempting to assume that students intuitively relate new concepts to their background knowledge, but this is not always the case, especially when they are novices. Having teachers review relevant material may also create the illusion of active prior knowledge. Rather, retrieval practice in the form of a short questionnaire on the required knowledge can be used as effective preparation for the learning, as well as a source of formative assessment for the teacher to understand whether students have retained relevant information.
3. Meaningful connections: create explicit and meaningful connections between prior knowledge and new concepts
The connections between the new concepts and existing knowledge should be explicit. After you have introduced and explained a new concept, you can establish these meaningful connections by using the elaborative interrogation method, which prompts students to explicitly and specifically explain the learned facts using questions like ‘why’ and ‘how’.
As connections are understood on the basis of already familiar connections, it is helpful to use familiar and well-grounded concrete examples that represent the type of connections being taught. The pyramid illustrations above are a concrete example of the relations between abstract concepts knowledge and understanding. Other concrete examples that teachers can use include:
- Real objects (such as fingers) as examples for number concepts
- Matrices of real objects as examples for the multiplication concept
- Visual or physical models to help explain scientific concepts like DNA, forces, or currents
In order to ensure that students are able to make meaningful connections between concepts by deeply understanding the concepts, it is important to use multiple concrete examples and make explicit links between them, explaining the features they have in common.
Implications for students with different backgrounds
It is clear that the background knowledge each student has acquired is the basis of their individual learning pyramids. This factor greatly influences how easily and how deeply they will engage in new learning. If students’ prior knowledge is well established, it will be easier for them to utilise, even without help from the teacher. However, when the background knowledge is shallow and not practised, it is unlikely that students will utilise it effectively and independently. This means that different students can be characterised as ‘quick learners’, ‘smart’ and even ‘creative’ just because they have gained more knowledge and it is better established in their minds. As students learn more, their ability to assimilate new knowledge grows – just like with pyramids, the wider the base, the higher you can reach.
As teachers we can take steps to support students’ learning by focusing on allocating their cognitive resources effectively. It is important to make sure that students gain new knowledge, understand it, and then practise it to reach mastery. While talk about 21st century skills tends to dominate current discourse about teaching and learning, research evidence makes it clear that knowledge, understanding and deliberate practice are still the basis for all knowledge and skill development. A teacher’s work is essential to making sure each student’s knowledge base is as solid as possible so that they can freely explore opportunities that we cannot even imagine.
Recommended further reading
Willingham, D. T. (2009). Why don’t students like school?: A cognitive scientist answers questions about how the mind works and what it means for the classroom. John Wiley & Sons.
It is based on research and written especially for teachers, includes clear explanation, compelling examples and demonstrations (some of which can be shared with students as well), and classroom applications. Specifically relevant are the following chapters:
Chapter 2: ‘Factual knowledge must precede skill’ on the importance of knowledge as building blocks.
Chapter 4: ‘We understand new things in the context of things we already know, and most of what we know is concrete’ on the importance of familiar concrete examples, deep knowledge and transfer.
References
Hirsch, E. D. (2003). Reading comprehension requires knowledge—of words and the world. American Educator, 27(1), 10-13. https://www.aft.org/sites/default/files/periodicals/Hirsch.pdf
The Learning Scientists. (2018, January). Concrete examples. Retrieved from https://www.learningscientists.org/learning-scientists-podcast/2018/1/3/episode-10-concrete-examples?rq=concrete%20examples
Willingham, D. T. (2007). Critical thinking. American Educator, 31(3), 8-19. https://www.aft.org/sites/default/files/periodicals/Crit_Thinking.pdf
Willingham, D. T. (2006). How knowledge helps: It speeds and strengthens reading comprehension, learning-and thinking. American Educator, 30(1), 30.
https://www.aft.org/periodical/american-educator/spring-2006/how-knowledge-helps
By Dr Efrat Furst

